By

文章目录
  1. 1. KNN算法
  2. 2. KD树
    1. 2.1. 建立KD树
    2. 2.2. KD树搜索
  3. 3. 栗子
  4. 4. 参考

KNN算法

给一个训练数据集和一个新的实例，在训练数据集中找出与这个新实例最近的k个训练实例，然后统计最近的k个训练实例中所属类别计数最多的那个类，就是新实例的类。

点我查看详情

但是该算法每次在查询k个最近邻的时候都需要遍历全集 才能计算出来，可想而且如果训练样本很大的话，代价还是很大的，那有没有啥方法可以优化呢？本文就针对KNN算法实现一个简单的KD树

KD树

KD树是一个二叉树，表示对K维空间的一个划分，可以进行快速检索（那KNN计算的时候不需要对全样本进行距离的计算了）

比如针对6个二维数据点{（2,3），（5,4），（9,6），（4,7），（8,1），（7,2）}，可以形成以下树形结构以及空间划分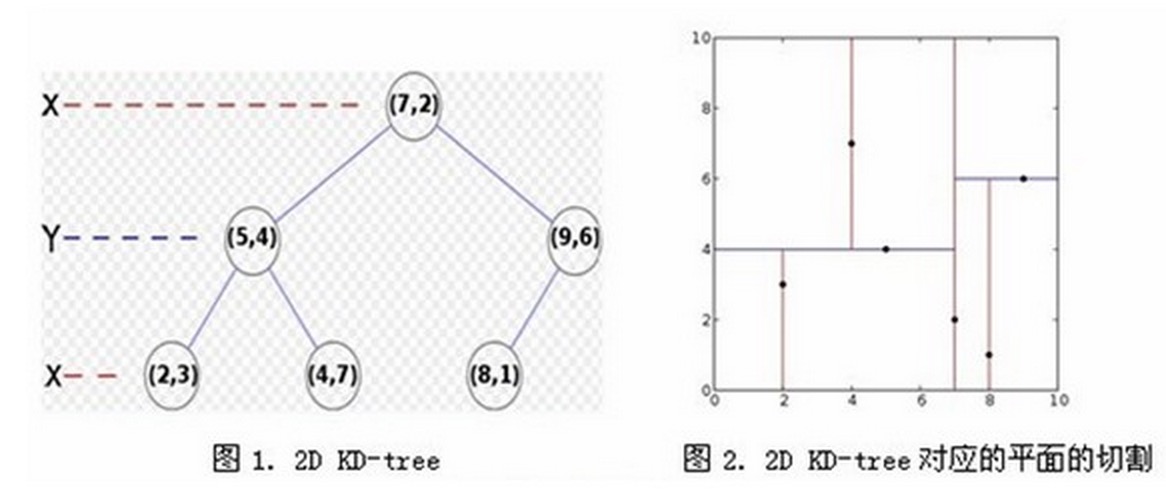

该树的功能就是在高维空间下进行一个快速的最近邻查询。先来看定义的树的类结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Node implements Comparable<Node>{
	public double[] data;//树上节点的数据  是一个多维的向量
	public double distance;//与当前查询点的距离  初始化的时候是没有的
	public Node left,right,parent;//左右子节点  以及父节点
	public int dim=-1;//维度  建立树的时候判断的维度
	
	public Node(double[] data)
	{
		this.data=data;
	}
	
	/**
	 * 返回指定索引上的数值
	 * @param index
	 * @return
	 */
	public double getData(int index)
	{
		if(data==null || data.length<=index)
			return Integer.MIN_VALUE;
		return data[index];
	}

	@Override
	public int compareTo(Node o) {
		if(this.distance>o.distance)
			return 1;
		else if(this.distance==o.distance)
			return 0;
		else return -1;
	}
	
	/**
	 * 计算距离 这里返回欧式距离
	 * @param that
	 * @return
	 */
	public double computeDistance(Node that)
	{
		if(this.data==null || that.data==null || this.data.length!=that.data.length)
			return Double.MAX_VALUE;//出问题了  距离最远
		double d=0;
		for(int i=0;i<this.data.length;i++)
		{
			d+=Math.pow(this.data[i]-that.data[i], 2);
		}
		
		return Math.sqrt(d);
	}
	
	public String toString()
	{
		if(data==null || data.length==0)
			return null;
		StringBuilder sb=new StringBuilder();
		for(int i=0;i<data.length;i++)
			sb.append(data[i]+" ");
		sb.append(" d:"+this.distance);
		return sb.toString();
	}
}

建立KD树

在d维的空间上循环找子区域的中位数进行划分的过程。
假设现在有d维空间的数据集T={x1,x2,x3,…xn},xi={a1,a2,a3..ad}

  1. 首先构造根节点，以坐标a1的中位数b为切分点，将根结点对应的矩形局域划分为两个区域，区域1中a1<b,区域2中a1>b，中位数所在的节点就是树上的节点
  2. 构造叶子节点，分别以上面两个区域中a2的中位数作为切分点，再次将他们两两划分，作为深度1的叶子节点，（如果a2=中位数，则a2的实例落在切分面）
  3. 不断重复2的操作，深度为j的叶子节点划分的时候，索取的ai 的i=j%d+1，直到两个子区域没有实例时停止

所以我们首先需要在高维的数据中针对某一维进行一个中位数的查找的，这里最快捷的就是借用快排的方法

假设f为快排的排头，进行一轮对比之后如果f所在的索引大于size/2，则此时只需要对左边进行递归排序就可以了，若小于size/2，则只需对右边区域进行递归排序，如果等于size/2  则说明
f就是中位数  直接返回就好啦

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * 使用快排进进行一个中位数的查找  完了之后返回的数组size/2即中位数
 * @param nodeList
 * @param index
 * @param left
 * @param right
 */
private void quickSortForMedian(List<Node> nodeList,int index,int left,int right)
{
	if(left>=right || nodeList.size()<=0)
		return ;
	
	Node kn=nodeList.get(left);
	double k=kn.getData(index);//取得向量指定索引的值
	
	int i=left,j=right;
	while(i<j)
	{
		while(nodeList.get(j).getData(index)>=k && i<j)
			j--;
		nodeList.set(i, nodeList.get(j));
		while(nodeList.get(i).getData(index)<=k && i<j)
			i++;
		nodeList.set(j, nodeList.get(i));
	}
	nodeList.set(i, kn);
	if(i==nodeList.size()/2)
		return ;//完成中位数的排序了
	else if(i<nodeList.size()/2)
	{
		quickSortForMedian(nodeList,index,i+1,right);//只需要排序右边就可以了
	}else{
		quickSortForMedian(nodeList,index,left,i-1);//只需要排序左边就可以了
	}
}

有了中位数查找，接下来就可以使用递归来进行树的建立了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * 构建kd树  返回根节点
 * @param nodeList
 * @param index
 * @return
 */
public Node buildKDTree(List<Node> nodeList,int index)
{
	if(nodeList==null || nodeList.size()==0)
		return null;
	quickSortForMedian(nodeList,index,0,nodeList.size()-1);//中位数排序
	Node root=nodeList.get(nodeList.size()/2);//中位数 当做根节点
	root.dim=index;
	List<Node> leftNodeList=new ArrayList<Node>();//放入左侧区域的节点  包括包含与中位数等值的节点-_-
	List<Node> rightNodeList=new ArrayList<Node>();
	
	for(Node node:nodeList)
	{
		if(root!=node)
		{
			if(node.getData(index)<=root.getData(index))
				leftNodeList.add(node);//左子区域 包含与中位数等值的节点
			else
				rightNodeList.add(node);
		}
	}
	
	int newIndex=index+1;//进入下一个维度
	if(newIndex>=root.data.length)
		newIndex=0;//从0维度开始再算
	root.left=buildKDTree(leftNodeList,newIndex);//添加左右子区域
	root.right=buildKDTree(rightNodeList,newIndex);
	
	if(root.left!=null)
		root.left.parent=root;//添加父指针  
	if(root.right!=null)
		root.right.parent=root;//添加父指针  
	return root;
}

KD树搜索

  1. 首先从根节点开始递归往下找到包含q的叶子节点，每一层都是找对应的xi
  2. 将这个叶子节点认为是当前的“近似最近点”
  3. 递归向上回退，如果以q圆心，以“近似最近点”为半径的球与根节点的另一半子区域边界相交，则说明另一半子区域中存在与q更近的点，则进入另一个子区域中查找该点并且更新”近似最近点“
  4. 重复3的步骤，直到另一子区域与球体不相交或者退回根节点
  5. 最后更新的”近似最近点“与q真正的最近点

这里注意按上述方式找到的与查询点最近的那个点，但是我们在KNN的时候是查询k个最近点，topK问题嘛，这里我们就使用了一个最大堆的维护来保证最近的k个点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
/**
 * 维护一个k的最大堆
 * @param listNode
 * @param newNode
 * @param k
 */
public void maintainMaxHeap(List<Node> listNode,Node newNode,int k)
{
	if(listNode.size()<k)
	{
		maxHeapFixUp(listNode,newNode);//不足k个堆   直接向上修复
	}else if(newNode.distance<listNode.get(0).distance){
		//比堆顶的要小   还需要向下修复 覆盖堆顶
		maxHeapFixDown(listNode,newNode);
	}
}

/**
 * 从上往下修复  将会覆盖第一个节点
 * @param listNode
 * @param newNode
 */
private void maxHeapFixDown(List<Node> listNode,Node newNode)
{
	listNode.set(0, newNode);
	int i=0;
	int j=i*2+1;
	while(j<listNode.size())
	{
		if(j+1<listNode.size() && listNode.get(j).distance<listNode.get(j+1).distance)
			j++;
		
		if(listNode.get(i).distance>=listNode.get(j).distance)
			break;
		
		Node t=listNode.get(i);
		listNode.set(i, listNode.get(j));
		listNode.set(j, t);
		
		i=j;
		j=i*2+1;
	}
}

private void maxHeapFixUp(List<Node> listNode,Node newNode)
{
	listNode.add(newNode);
	int j=listNode.size()-1;
	int i=(j+1)/2-1;//i是parent节点
	while(i>=0)
	{
		
		if(listNode.get(i).distance>=listNode.get(j).distance)
			break;
		
		Node t=listNode.get(i);
		listNode.set(i, listNode.get(j));
		listNode.set(j, t);
		
		j=i;
		i=(j+1)/2-1;
	}
}

好，现在就可以按照上述的思路来进行搜索了，搜索过程中维护一个k堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
/**
 * 查询最近邻
 * @param root kd树
 * @param q 查询点
 * @param k
 * @return
 */
public List<Node> searchKNN(Node root,Node q,int k)
{
	List<Node> knnList=new ArrayList<Node>();
	Node almostNNode=searchLeaf(root,q);//近似最近点

	
	while(almostNNode!=null)
	{
		double curD=q.computeDistance(almostNNode);//最近近似点与查询点的距离 也就是球体的半径
		almostNNode.distance=curD;
		maintainMaxHeap(knnList,almostNNode,k);
		if(almostNNode.parent!=null &&
				curD>Math.abs(q.getData(almostNNode.parent.dim)-almostNNode.parent.getData(almostNNode.parent.dim)))
		{
			//这样可能在另一个子区域中存在更加近似的点
			Node brother=getBrother(almostNNode);
			brother.distance=q.computeDistance(brother);
			maintainMaxHeap(knnList,brother,k);
		}
		
		almostNNode=almostNNode.parent;//返回上一级
	}
	
	return knnList;
}

/**
 * 获取兄弟节点
 * @param node
 * @return
 */
public Node getBrother(Node node)
{
	if(node==node.parent.left)
		return node.parent.right;
	else
		return node.parent.left;
}

/**
 * 查询到叶子节点
 * @param root
 * @param q
 * @return
 */
public Node searchLeaf(Node root,Node q)
{
	Node leaf=root,next=null;
	int index=0;
	while(leaf.left!=null || leaf.right!=null)
	{
		if(q.getData(index)<leaf.getData(index))
		{
			next=leaf.left;//进入左侧
		}else if(q.getData(index)>leaf.getData(index))
		{
			next=leaf.right;
		}else{
			//当取到中位数时  判断左右子区域哪个更加近
			if(q.computeDistance(leaf.left)<q.computeDistance(leaf.right))
				next=leaf.left;
			else
				next=leaf.right;
		}
		if(next==null)
			break;//下一个节点是空时  结束了
		else{
			leaf=next;
			if(++index>=root.data.length)
				index=0;
		}
	}
	
	return leaf;
}

注意这里在判断查询点q与另一个子区域的边界是否相交时是需要判断半径与（q和父节点影响构建维数上的值之差即可）

栗子

还是以上面的6个数据点进行构建

1
2
3
4
5
6
7
8
9
10
11
List<Node> nodeList=new ArrayList<Node>();
nodeList.add(new Node(new double[]{2,3}));
nodeList.add(new Node(new double[]{5,4}));
nodeList.add(new Node(new double[]{9,6}));
nodeList.add(new Node(new double[]{4,7}));
nodeList.add(new Node(new double[]{8,1}));
nodeList.add(new Node(new double[]{7,2}));

KDTree kdTree=new KDTree();
Node root=kdTree.buildKDTree(nodeList,0);
System.out.println(root);

对(2.1,3.1)进行查询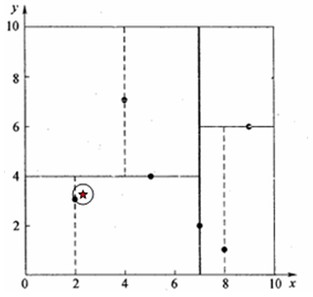

1
System.out.println(kdTree.searchKNN(root,new Node(new double[]{2.1,3.1}),2));

可以发现最近的两个点

[5.0 4.0  d:3.0364452901377956, 2.0 3.0  d:0.14142135623730964]

完全符合预期

再来看(2,4.5)这个查询点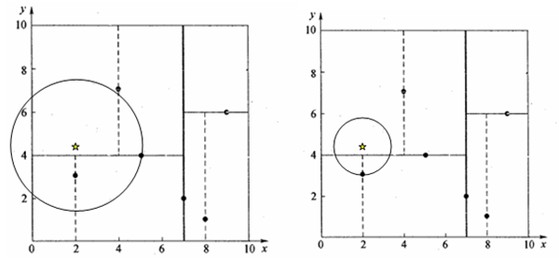

1
2
System.out.println(kdTree.searchKNN(root,new Node(new double[]{2,4.5}),1));
System.out.println(kdTree.searchKNN(root,new Node(new double[]{2,4.5}),3));

[2.0 3.0  d:1.5]
[4.0 7.0  d:3.2015621187164243, 2.0 3.0  d:1.5, 5.0 4.0  d:3.0413812651491097]

首先最近邻的叶子节点是(4,7) 但是其半径会与另一子区域相交，所以继续进行(2,3)进行距离计算

完整的源代码在这儿有!

参考

  1. 《统计学习方法》第三章
  2. http://blog.csdn.net/qll125596718/article/details/8426458这篇文章举例比较详细

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。

文章目录
  1. 1. KNN算法
  2. 2. KD树
    1. 2.1. 建立KD树
    2. 2.2. KD树搜索
  3. 3. 栗子
  4. 4. 参考